---

1 2 3 4

El M.A.S., un movimiento periódico

Periodo y frecuencia

firmar que un movimiento es periódico equivale a decir que se repite a sí mismo a intervalos iguales de tiempo, o en otros términos, que todas sus magnitudes características como la posición, la velocidad o la aceleración toman valores iguales a otros valores anteriores cada cierto periodo de tiempo.

El movimiento circular uniforme es el caso más sencillo de movimiento periódico. Después de cada vuelta el movimiento vuelve a ser idéntico al de la vuelta anterior y así sucesivamente. El tiempo empleado en describir una vuelta completa se denomina periodo y se representa por la letra T. El número de vueltas o revoluciones que se dan en un segundo recibe el nombre de frecuencia y se representa mediante la letra f. La frecuencia y el periodo están relacionados en la forma:

(7.1)

El periodo T equivale a número de segundos por vuelta y se expresa en segundos; la frecuencia (f) equivale a número de vueltas por segundo y se expresa en ciclos/segundo o hertzs (Hz).

La relación del periodo T con la velocidad angular w en el movimiento circular viene dada por la ecuación:

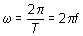
(7.2)

pues en T segundos el punto móvil barre un ángulo de 2p radianes, es decir, da una vuelta completa.

Dado que el M.A.S., según su definición, es la proyección de otro movimiento periódico (circular uniforme), ha de ser por ello también periódico. El periodo T representa, en este caso, el tiempo que corresponde a una oscilación completa y la frecuencia f el número de oscilaciones por segundo. Por la misma razón ambas magnitudes toman valores idénticos a los del movimiento circular auxiliar.

Posición

El estudio matemático de la variación de la posición del punto vibrante P, con el tiempo, se puede efectuar determinando el valor de la proyección del punto asociado Q correspondiente al movimiento circular auxiliar. Para ello, se dibuja un sistema de ejes XY haciendo coincidir el eje horizontal con la trayectoria rectilínea del M.A.S. Si se toma como origen de ángulos el eje vertical, la coordenada del punto vibrante, de acuerdo con la definición trigonométrica del seno, vendrá dada por:

X = R . sen f
(7.3)

donde R es el radio del movimiento circular auxiliar y f el ángulo correspondiente al arco descrito.

Puesto que f se refiere a un movimiento circular uniforme, se cumplirá la relación:

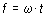
siendo w la velocidad angular característica.

Cuando el radio R se mide a lo largo de la trayectoria del M. A. S., se representa mediante la letra A, con lo cual la ecuación (7.3) toma la forma:

(7.4)

La coordenada x que define, según la ecuación anterior, la posición del punto vibrante respecto del origen O se denomina, en este tipo de movimientos, elongación. Su valor varía con el tiempo entre dos valores extremos A y -A en forma sinusoidal. A constituye, por tanto, el valor máximo de la elongación y se denomina amplitud. Equivale a la altura de la gráfica sinusoidal que representa la variación de x con t. El hecho de que en la ecuación (7.4) que define el M.A.S. aparezca la función seno, da origen al calificativo armónico, pues éste es el nombre que reciben las funciones trigonométricas seno y coseno. El ángulo j recibe el nombre de ángulo de fase, o simplemente fase del M. A. S. y a w se la conoce también por frecuencia angular o pulsación.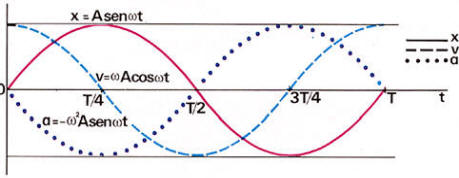

Las gráficas cinemáticas de variación de la posición, de la velocidad y de la aceleración con el tiempo están representadas por tres líneas sinusoidales.

Cuando se sustituye el valor de w dado por la ecuación (7.2) en la expresión (7.4) de la elongación resulta:

(7.5)

o bien:

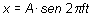
(7.6)

Estas nuevas ecuaciones de la elongación de un movimiento armónico simple tienen la virtud de que los dos parámetros o constantes características que aparecen en ellas, a saber, la amplitud A y el periodo T o en su caso la frecuencia f, se refieren sólo y exclusivamente al M.A.S. Se evita, de este modo, la referencia explícita a través de al movimiento circular auxiliar. Conocidas, por tanto, la amplitud A y la frecuencia f (o el periodo T) de un M.A.S. éste queda perfectamente caracterizado.

1 2 3 4

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios